Topos (Mathematik)

Topos (pl. Topoi, griech. Ort) ist ein Begriff der Kategorientheorie, der in zwei engverwandten Ausprägungen vorkommt, nämlich

• als Elementartopos, der eine verallgemeinerte Kategorie aller Mengen ist, mit dem Ziel einer nicht-mengentheoretischen Grundlegung der Mathematik.
• als Grothendieck-Topos, der ein verallgemeinerter topologischer Raum ist und Anwendungen in der algebraischen Geometrie findet.

Die Idee eines Elementartopos geht ursprünglich auf William Lawvere (1937–2023) zurück, welcher sich 1963 zum Ziel setzte, die Mathematik auf ein rein kategorientheoretisches Fundament zu stellen (anstatt der bis heute üblichen Mengenlehre). In Zusammenarbeit mit Myles Tierney formulierte er gegen Ende der 1960er Jahre schließlich die Axiome für einen Elementartopos. Dieses ist, vereinfacht gesagt, eine Art Universum (informell gesprochen), in dem es möglich ist, Mathematik zu betreiben. Ein Elementartopos enthält genügend Struktur, um darin einen abstrakten Mengenbegriff zu definieren und damit Mathematik und Logik zu betreiben. Insbesondere besitzt ein Elementartopos eine sogenannte interne Logik, welche nicht unbedingt klassisch sein muss.

Ein Elementartopos ist eine Kategorie ${\displaystyle {\mathcal {E}}}$ mit

• (a) einem Pullback für jedes Diagramm ${\displaystyle A\to X\leftarrow B}$;
• (b) einem terminalen Objekt ${\displaystyle 1}$;
• (c) einem Objekt ${\displaystyle \Omega }$, genannt der Unterobjekt-Klassifizierer (wörtlich von engl. subobject classifier) und einem Monomorphismus ${\displaystyle \mathrm {true} \colon 1\rightarrowtail \Omega }$, sodass für jeden Monomorphismus ${\displaystyle m\colon A\rightarrowtail B}$ ein eindeutiger Pfeil ${\displaystyle \chi _{m}\colon B\to \Omega }$ (genannt der Charakter von ${\displaystyle m}$) existiert, sodass folgendes Diagramm ein Pullback ist:

wobei hier ${\displaystyle !\colon A\to 1}$ den eindeutigen Pfeil von ${\displaystyle A}$ ins Terminalobjekt ${\displaystyle 1}$ bezeichne;

• (d) einem Exponential ${\displaystyle C^{A}}$ mit zugehörigem Evaluations-Pfeil ${\displaystyle \mathrm {ev} _{C,A}:C^{A}\times A\to C}$ für je zwei Objekte ${\displaystyle A,C}$, mit der universellen Eigenschaft, dass für jedes Objekt ${\displaystyle B}$ und jeden Pfeil ${\displaystyle f\colon B\times A\to C}$ genau ein Pfeil ${\displaystyle f'\colon B\to C^{A}}$ existiert, sodass folgendes Diagramm kommutiert:

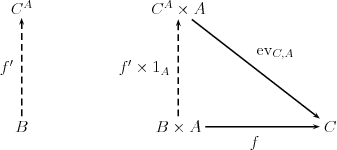
wobei ${\displaystyle 1_{A}\colon A\to A}$ den Identitätspfeil von ${\displaystyle A}$ bezeichne.

Die Eigenschaften (a) und (b) lassen sich kurz zusammenfassen, indem man sagt ${\displaystyle {\mathcal {E}}}$ sei endlich vollständig (d. h. alle endlichen Limites existieren). Die Eigenschaften (c) und (d) scheinen im ersten Moment extrem künstlich und abstrakt zu sein, sind jedoch beide durch die Kategorie ${\displaystyle \mathbf {Sets} }$ aller Mengen motiviert. Kürzer schreibt man oft für (d), dass der Funktor ${\displaystyle -\times A\colon {\mathcal {E}}\to {\mathcal {E}}}$ für alle ${\displaystyle A}$ einen Rechtsadjungierten (meist mit ${\displaystyle (-)^{A}}$ bezeichnet) besitzt.

Die ursprüngliche Definition eines Elementartopos enthielt auch die Forderung, dass dieser endlich ko-vollständig sein soll (d. h., dass alle endlichen Kolimites existieren). Diese Forderung folgt jedoch, nach einem nicht-trivialen Resultat von Mikkelsen.^[1]

Wie schon gesagt, sollte mit Hilfe der Topostheorie ein kategorientheoretisches Fundament für die Mathematik gelegt werden. Dies bedeutet insbesondere, dass die Kategorie ${\displaystyle \mathbf {Sets} }$ aller Mengen dadurch beschrieben werden muss. Entsprechend ist dies wohl auch das wichtigste Beispiel, was die Motivation der verschiedenen Konzepte der Topostheorie angeht. In ${\displaystyle \mathbf {Sets} }$ ist ${\displaystyle C^{A}=\{f\colon A\to C\}}$ schlicht die Menge aller Abbildungen von ${\displaystyle A}$ nach ${\displaystyle C}$ und entsprechend ${\displaystyle \mathrm {ev} _{C,A}\colon C^{A}\times A\to C,(f,a)\mapsto f(a)}$. Weiter ist ${\displaystyle \Omega =\{0,1\}=2}$ (man beachte, dass hier ${\displaystyle 2}$ als finite Ordinalzahl zu verstehen ist), ${\displaystyle \mathrm {true} :\{0\}\to \{0,1\},0\mapsto 1}$ und ${\displaystyle \chi _{m}\colon B\to \{0,1\},b\mapsto \left\{{\begin{array}{ll}0&b\notin A\\1&b\in A\end{array}}\right.}$ die übliche charakteristische Funktion von ${\displaystyle A}$ als Teilmenge von ${\displaystyle B}$.

Die Eigenschaft, dass ${\displaystyle \Omega }$ nur zwei Elemente enthält bedeutet, dass es sich bei ${\displaystyle \mathbf {Sets} }$ um einen sogenannten booleschen Topos handelt und dieser ist elementar für die klassische Mathematik (klassisch im Sinne von nicht-intuitionistisch).

Um ${\displaystyle \mathbf {Sets} }$ abstrakt gegenüber allgemeinen Elementartopoi auszuzeichnen, werden gewöhnlich die folgenden Axiome verwendet.^[2]

• Es gibt ein Anfangsobjekt ${\displaystyle 0\not \cong 1}$ (Nichttrivialität).
• Sind ${\displaystyle f,g\colon X\to Y}$ Pfeile, so ist ${\displaystyle f=g}$ oder es existiert ein ${\displaystyle x\colon 1\to X}$ mit ${\displaystyle f\circ x\neq g\circ x}$ (Wohlpunktiertheit).
• Es gibt ein Objekt natürlicher Zahlen, d. h. ein Objekt ${\displaystyle N}$ zusammen mit Pfeilen

${\displaystyle 1{\stackrel {z}{\longrightarrow }}N{\stackrel {s}{\longrightarrow }}N,}$

sodass für jedes Objekt ${\displaystyle X}$ mit Pfeilen ${\displaystyle 1{\stackrel {x}{\longrightarrow }}X{\stackrel {f}{\longrightarrow }}X}$ ein eindeutig bestimmter Pfeil ${\displaystyle h\colon N\to X}$ existiert mit ${\displaystyle h\circ z=x}$ und ${\displaystyle h\circ s=f\circ h}$.

• Für jeden Epimorphismus ${\displaystyle e\colon X\to Y}$ existiert ein Pfeil ${\displaystyle m\colon Y\to X}$ mit ${\displaystyle e\circ m=1_{Y}}$ (Auswahlaxiom).

Ein Grothendieck-Topos ist definiert als eine Kategorie, die äquivalent ist zur Kategorie der Garben (von Mengen) auf einem Situs. Nach einem Satz von Jean Giraud ist eine Kategorie ${\displaystyle {\mathcal {E}}}$ genau dann ein Grothendieck-Topos, wenn die folgenden Eigenschaften erfüllt sind:

• (a) In ${\displaystyle {\mathcal {E}}}$ existieren endliche projektive Limites.
• (b) In ${\displaystyle {\mathcal {E}}}$ existieren beliebige Koprodukte, und sie sind universell disjunkt.

Ein Koprodukt ${\displaystyle \textstyle S=\coprod _{i}S_{i}}$ heißt disjunkt, wenn die Strukturmorphismen ${\displaystyle S_{i}\to S}$ Monomorphismen sind und ${\displaystyle S_{i}\times _{S}S_{j}}$ für ${\displaystyle i\neq j}$ ein Anfangsobjekt ist. Das Koprodukt heißt universell disjunkt, wenn es unter jedem Basiswechsel ${\displaystyle T\to S}$ disjunkt bleibt, das heißt, wenn ${\displaystyle \textstyle T=\coprod _{i}(T\times _{S}S_{i})}$ disjunkt ist.

• (c) Äquivalenzrelationen in ${\displaystyle {\mathcal {E}}}$ sind universell effektiv.

Dabei ist eine Äquivalenzrelation ein Paar ${\displaystyle p_{1},p_{2}\colon R\to X}$ von Morphismen, so dass für jedes Objekt ${\displaystyle T\in \mathrm {Ob} ({\mathcal {E}})}$ die induzierte Abbildung ${\displaystyle (p_{1},p_{2})\colon R(T)\to X(T)\times X(T)}$ eine Bijektion auf den Graphen einer Äquivalenzrelation auf ${\displaystyle X(T)}$ ist. Dabei ist ${\displaystyle X(T):=\operatorname {Hom} (T,X)}$.

• (d) ${\displaystyle {\mathcal {E}}}$ besitzt eine erzeugende Familie von Objekten.

Dabei heißt eine Familie ${\displaystyle (E_{i})_{i\in I}}$ von Objekten erzeugend, wenn ein Morphismus ${\displaystyle X\to Y}$, für den alle induzierten Abbildungen ${\displaystyle X(E_{i})\to Y(E_{i})}$ Bijektionen sind, ein Isomorphismus ist.

Es sei angemerkt, dass jeder Grothendieck-Topos immer auch ein Elementartopos ist.

• Michael Artin, Alexander Grothendieck, Jean-Louis Verdier: Séminaire de géométrie algébrique du Bois-Marie. Théorie des topos et cohomologie étale des schémas. (SGA 4) 1963–64.
• Francis Borceux: Handbook of Categorical Algebra 3: Categories of Sheaves. Cambridge, 1994.
• Rob Goldblatt: Topoi: the categorial analysis of logic. 1. Auflage. Amsterdam 1979. 2. Auflage. Mineola NY 1984. Dover Publications, 2006, ISBN 0-486-45026-0, Zbl 0434.03050 (krit. bespr. v. Johnstone) Scans
• William Lawvere, Robert Rosebrugh: Sets for Mathematics. Cambridge University Press, 2003.
• Saunders Mac Lane, Ieke Moerdijk: Topos theory. In: M. Hazewinkel (Hrsg.): Handbook of algebra. Amsterdam 1996, ISBN 0-444-82212-7, Band I, S. 501–528, Zbl 0858.18001
• Saunders Mac Lane, Ieke Moerdijk: Sheaves in geometry and logic: a first introduction to topos theory. Universitext, Berlin 1992, ISBN 0-387-97710-4. xii, 627 p., Zbl 0822.18001
• Michael Barr, Charles Frederick Wells: Toposes, Triples and Theories. – Berlin, 1983 (Grundlehren der math. Wissenschaften; 278).
• Peter T. Johnstone: Sketches of an Elephant: A Topos Theory Compendium. Oxford Logic Guides, 43 & 44, 2002, ISBN 0-19-852496-X, Zbl 1071.18002
• Ieke Moerdijk, Jacob Johan Caspar Vermeulen: Proper Maps of Toposes. In: Mem. Am. Math. Soc., 705, 2000, ISBN 0-8218-2168-7, Zbl 0961.18003

1. ↑ Robert Paré: Colimits in topoi. In: Bull. Amer. Math. Soc., 80, 1974, S. 556–561.
2. ↑ Colin McLarty: Elementary Categories, Elementary Toposes. Oxford University Press, 2005, ISBN 0-19-851473-5, S. 211,213.