Essentially surjective functor

In mathematics, specifically in category theory, a functor

F : C → D {\displaystyle F:C\to D}

is essentially surjective if each object d {\displaystyle d} of D {\displaystyle D} is isomorphic to an object of the form F c {\displaystyle Fc} for some object c {\displaystyle c} of C {\displaystyle C} .

Any functor that is part of an equivalence of categories is essentially surjective. As a partial converse, any full and faithful functor that is essentially surjective is part of an equivalence of categories.[1]

Notes

  1. ^ Mac Lane (1998), Theorem IV.4.1

References

  • Mac Lane, Saunders (September 1998). Categories for the Working Mathematician (second ed.). Springer. ISBN 0-387-98403-8.
  • Riehl, Emily (2016). Category Theory in Context. Dover Publications, Inc Mineola, New York. ISBN 9780486809038.

External links

  • Essentially surjective functor at the nLab
  • v
  • t
  • e
Functor types
  • Additive
  • Adjoint
  • Conservative
  • Derived
  • Diagonal
  • Enriched
  • Essentially surjective
  • Exact
  • Forgetful
  • Full and faithful
  • Logical
  • Monoidal
  • Representable
  • Smooth


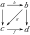Stub icon

This category theory-related article is a stub. You can help Wikipedia by expanding it.

  • v
  • t
  • e