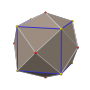
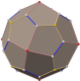
Rhombicuboctahedron

Rhombicuboctahedron
Type	Archimdean Uniform polyhedron
Faces	8 equilateral triangles 18 squares
Edges	48
Vertices	24
Vertex configuration	${\displaystyle 24(3\cdot 4^{3})}$
Schläfli symbol	${\displaystyle r{\begin{Bmatrix}3\\4\end{Bmatrix}}}$
Symmetry group	Octahedral symmetry ${\displaystyle \mathrm {O} _{\mathrm {h} }}$ Pyritohedral symmetry ${\displaystyle \mathrm {T} _{\mathrm {h} }}$
Dihedral angle (degrees)	square-to-square: 135° square-to-triangle: 144.7°
Dual polyhedron	Deltoidal icositetrahedron
Vertex figure
Net

In geometry, rhombicuboctahedron is an Archimedean solid with 24 faces, consisting of 8 equilateral triangles and 18 squares. It is named by Johannes Kepler in his 1618 Harmonices Mundi, being short for truncated cuboctahedral rhombus, with cuboctahedral rhombus being his name for a rhombic dodecahedron.^[1]

The rhombicuboctahedron is an Archimedean solid, and it has Catalan solid as its dual, deltoidal icositetrahedron. The elongated square gyrobicupola is the polyhedron that is similar to a rhombicuboctahedron, but it is not an Archimedean solid because it is not vertex-transitive. The skeleton of a rhombicuboctahedron can be represented as a graph known as rhombicuboctahedral graph. The rhombicuboctahedron may be found in many popular cultures as in architecture, toys, and arts.

Construction

The rhombicuboctahedron may be constructed from a cube by drawing a smaller one in the middle of each face, parallel to the cube's edges. After removing the edges of a cube, the squares may be joined by adding more squares adjacent between them, and the corners may be filled by the equilateral triangles. Another way to construct the rhombicuboctahedron is by attaching two regular square cupolas into the bases of a regular octagonal prism.^[2]

A rhombicuboctahedron may also be known as an expanded octahedron or expanded cube. This is because the rhombicuboctahedron may also be constructed by separating and pushing away the faces of a cube or a regular octahedron from their centroid (in blue or red, respectively, in the animation), and filling between them with the squares and equilateral triangles. This construction process is known as expansion.^[3] By using all of these methods above, the rhombicuboctahedron has 8 equilateral triangles and 16 squares as its faces.^[4]

One way to construct the rhombicuboctahedron by Cartesian coordinates with an edge length 2 is. ${\displaystyle \left(\pm \left(1+{\sqrt {2}}\right),\pm 1,\pm 1\right)}$. ^[5]

Properties

Measurement and metric properties

A rhombicuboctahedron with edge length ${\displaystyle a}$ has a surface area:^[6]

by adding the area of 8 equilateral triangles and 10 squares. Its volume can be calculated by slicing it into two square cupolas and one octagonal prism:^[6]

The optimal packing fraction of rhombicuboctahedra is given by

It was noticed that this optimal value is obtained in a Bravais lattice by de Graaf, van Roij & Dijkstra (2011).^[7] Since the rhombicuboctahedron is contained in a rhombic dodecahedron whose inscribed sphere is identical to its inscribed sphere, the value of the optimal packing fraction is a corollary of the Kepler conjecture: it can be achieved by putting a rhombicuboctahedron in each cell of the rhombic dodecahedral honeycomb, and it cannot be surpassed, since otherwise the optimal packing density of spheres could be surpassed by putting a sphere in each rhombicuboctahedron of the hypothetical packing which surpasses it.^{[citation needed]}

The dihedral angle of a rhombicuboctahedron can be determined by adding the dihedral angle of a square cupola and an octagonal prism:^[8]

• the dihedral angle of a rhombicuboctahedron between two adjacent squares on both the top and bottom are that of a square cupola 135°. The dihedral angle of an octagonal prism between two adjacent squares is the internal angle of a regular octagon 135°. The dihedral angle between two adjacent squares on the edge where a square cupola is attached to an octagonal prism is the sum of the dihedral angle of a square cupola square-to-octagon and the dihedral angle of an octagonal prism square-to-octagon 45° + 90° = 135°. Therefore, the dihedral angle of a rhombicuboctahedron for every two adjacent squares is 135°.
• the dihedral angle of a rhombicuboctahedron square-to-triangle is that of a square cupola between those 144.7°. The dihedral angle between square-to-triangle, on the edge where a square cupola is attached to an octagonal prism is the sum of the dihedral angle of a square cupola triangle-to-octagon and the dihedral angle of an octagonal prism square-to-octagon 54.7° + 90° = 144.7°. Therefore, the dihedral angle of a rhombicuboctahedron for every square-to-triangle is 144.7°.

Symmetry and its classification family

The rhombicuboctahedron has the same symmetry as a cube and regular octahedron, the octahedral symmetry ${\displaystyle \mathrm {O} _{\mathrm {h} }}$.^[9] However, the rhombicuboctahedron also has a second set of distortions with six rectangular and sixteen trapezoidal faces, which do not have octahedral symmetry but rather pyritohedral symmetry ${\displaystyle \mathrm {T} _{\mathrm {h} }}$, so they are invariant under the same rotations as the tetrahedron but different reflections.^[10] It is centrosymmetric, meaning its symmetric is interchangeable by the appearance of inversion center. It is also non-chiral; that is, it is congruent to its own mirror image.^[11]

The rhombicuboctahedron is an Archimedean solid, meaning it is a highly symmetric and semi-regular polyhedron, and two or more different regular polygonal faces meet in a vertex.^[12] Its dual is deltoidal icositetrahedron, a Catalan solid, shares the same symmetry as the rhombicuboctahedron.^{[citation needed]} A rhombicuboctahedron is one of the Archimedean solids with the Rupert property, meaning there is a polyhedron with the same or larger size that can pass through its hole.^[13]

The elongated square gyrobicupola is the only polyhedron resembling the rhombicuboctahedron. The difference is that the elongated square gyrobicupola is constructed by twisting one of its cupolae. It was once considered as the 14th Archimedean solid, until it was discovered that it is vertex-transitive, categorizing it as the Johnson solid instead.^[14]

Rhombicuboctahedral graph

The rhombicuboctahedral graph is a graph representing the skeleton of a rhombicuboctahedron. It is polyhedral graph, meaning that it is planar and 3-vertex-connected. In other words, the edges of a graph are not crossed while being drawn, and removing any two of its vertices leaves a connected subgraph. It has 24 vertices and 48 edges. It is a quartic, meaning each of its vertices is connected by four vertices. This graph is classified as Archimedean graph, because it resembles the graph of Archimedean solid.^[15]

Appearances

The rhombicuboctahedron appears in the architecture, with an example of the building is the National Library located at Minsk.^[16]

The rhombicuboctahedron may also be found in toys. An example is the lines along which a Rubik's Cube can be turned are, projected onto a sphere, similar, topologically identical, to a rhombicuboctahedron's edges. Variants using the Rubik's Cube mechanism have been produced, which closely resemble the rhombicuboctahedron. During the Rubik's Cube craze of the 1980s, at least two twisty puzzles sold had the form of a rhombicuboctahedron (the mechanism was similar to that of a Rubik's Cube)^[17][18] Another example may be found in dice from Corfe Castle, each of which square faces have marks of pairs of letters and pips.^[19]

The rhombicuboctahedron may also appear in the art. An example is the 1495 Portrait of Luca Pacioli, traditionally attributed to Jacopo de' Barbari, which includes a glass rhombicuboctahedron half-filled with water, which may have been painted by Leonardo da Vinci.^[21] The first printed version of the rhombicuboctahedron was by Leonardo and appeared in Pacioli's Divina proportione (1509).

A spherical 180° × 360° panorama can be projected onto any polyhedron; but the rhombicuboctahedron provides a good enough approximation of a sphere while being easy to build. This type of projection, called Philosphere, is possible from some panorama assembly software. It consists of two images printed separately and cut with scissors while leaving some flaps for assembly with glue.^[22]

References

Notes

Works cited

See also

• Compound of five rhombicuboctahedra
• Cube
• Cuboctahedron
• Nonconvex great rhombicuboctahedron
• Truncated rhombicuboctahedron
• Elongated square gyrobicupola
• Moravian star
• Octahedron
• Rhombicosidodecahedron
• Rubik's Snake – puzzle that can form a Rhombicuboctahedron "ball"
• National Library of Belarus – its architectural main component has the shape of a rhombicuboctahedron.
• Truncated cuboctahedron (great rhombicuboctahedron)

Further reading

External links

• Weisstein, Eric W., "Rhombicuboctahedron" ("Archimedean solid") at MathWorld.
  • Weisstein, Eric W. "Small rhombicuboctahedral graph". MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra x3o4x - sirco".
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• Editable printable net of a rhombicuboctahedron with interactive 3D view
• Rhombicuboctahedron Star by Sándor Kabai, Wolfram Demonstrations Project.
• Rhombicuboctahedron: paper strips for plaiting