自動微分

自動微分（じどうびぶん、英: automatic differentiation, autodiff, AD）やアルゴリズム微分（英: algorithmic differentiation）とは、プログラムで定義された関数を解析し、関数の値と同時に偏導関数の値を計算するアルゴリズムである。

自動微分は複雑なプログラムであっても加減乗除などの基本的な算術演算や基本的な関数（指数関数・対数関数・三角関数など）のような基本的な演算の組み合わせで構成されていることを利用し、これらの演算に対して合成関数の偏微分の連鎖律を繰り返し適用することによって実現される。自動微分を用いることで偏導関数値を少ない計算量で自動的に求めることができる。

他の微分方式との違い

自動微分は以下のどちらとも異なる。

• 記号微分・数式微分（symbolic differentiation） - 原関数を表す数式から数式処理により導関数を導出する。数式処理システムで実装されている。
• 数値微分（numerical differentiation） - 原関数の値から数値的に微分係数を算出する

記号微分は効率が悪くなりやすく、プログラムで定義された関数から微分表現を導くのは困難であるという問題がある。一方、数値微分では離散化の際の丸め誤差や桁落ちによる精度の低下が問題である。さらに、どちらの手法も計算量や誤差の関係で高次の微分係数を求めることが難しい。また、勾配を用いた最適化で必要となる、多くの入力変数を持つ関数に対する偏微分値の計算を行うには速度が遅い。自動微分はこれらの古典的手法の問題を解決する。^[1]

また、自動微分は計算フローを追いかけることで計算できるので、分岐（if文）やループや再帰を含むようなアルゴリズムでも偏微分できる^[1]。

自動微分の導出

合成関数の偏微分の連鎖律

自動微分の基本原理は、合成関数の偏微分の連鎖律を用いた偏微分の分解である。

合成関数の偏微分の連鎖律とは ${\displaystyle y=f(w_{1},w_{2}),w_{1}=g(x_{1},x_{2}),w_{2}=h(x_{1},x_{2})}$ の時、下記が成立することである^[2][3]。

${\displaystyle {\frac {\partial y}{\partial x_{1}}}={\frac {\partial y}{\partial w_{1}}}{\frac {\partial w_{1}}{\partial x_{1}}}+{\frac {\partial y}{\partial w_{2}}}{\frac {\partial w_{2}}{\partial x_{1}}}}$

2種類の自動微分

自動微分は2種類に分けられ、それぞれ

• ボトムアップ型自動微分（フォーワード・モード、フォーワード・アキュムレーション、タンジェント・モード、狭義の自動微分）
• トップダウン型自動微分（リバース・モード、リバース・アキュムレーション、随伴モード、高速自動微分）

と呼ばれる。

ボトムアップ型自動微分では連鎖律を内側から外側に計算し（∂w/∂xを計算した後で ∂y/∂w を計算する）、トップダウン型自動微分では外側から内側に計算する。

使い分けは、入力が n 次元、出力が m 次元とした場合、以下の違いがある。

• n < m ならばボトムアップ型の方が計算量が少ない。ボトムアップ型の計算回数はn回。
• n > m ならばトップダウン型の方が計算量が少ない。トップダウン型の計算回数はm回。

機械学習において、評価値はほぼ常に m = 1 の実数なので、トップダウン型が使われる。機械学習で用いられる多層パーセプトロンのバックプロパゲーションはトップダウン型自動微分の特殊なケースである。

ボトムアップ型はR.E. Wengertが1964年に発表したが、2ページの論文で特に名前を付けていない^[4]。Andreas Griewank によると、トップダウン型を誰が最初に発明したのか判然としないが、計算量を減らす工夫として1960年代後半には提案されていた^[5]。

ボトムアップ型自動微分

ボトムアップ型自動微分では最初に偏微分を行う入力変数を固定し、それぞれの部分式を再帰的に計算する。手計算においては連鎖律において内側の関数を繰り返し置き換えていくことに相当する。

${\displaystyle {\frac {\partial y}{\partial x}}={\frac {\partial y}{\partial w_{1}}}{\frac {\partial w_{1}}{\partial x}}={\frac {\partial y}{\partial w_{1}}}\left({\frac {\partial w_{1}}{\partial w_{2}}}{\frac {\partial w_{2}}{\partial x}}\right)={\frac {\partial y}{\partial w_{1}}}\left({\frac {\partial w_{1}}{\partial w_{2}}}\left({\frac {\partial w_{2}}{\partial w_{3}}}{\frac {\partial w_{3}}{\partial x}}\right)\right)=\cdots }$

多変数の場合はヤコビ行列の積として一般化できる。

トップダウン型自動微分と比較すると、ボトムアップ型自動微分は自然であり、偏微分に関する情報の流れが計算の順序と一致するため簡単に実行できる。それぞれの変数にその偏導関数値 ${\displaystyle {\dot {w}}_{i}}$

${\displaystyle {\dot {w}}_{i}={\frac {\partial w_{i}}{\partial x}}}$

の計算値を保存する領域を付け加えるだけで、変数値の計算と同時に偏導関数値を計算することができる。

連鎖律より、${\displaystyle w_{i}}$ が計算グラフで先行ノードを持つ場合、

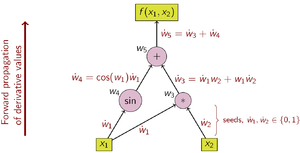
${\displaystyle {\dot {w}}_{i}=\sum _{j}{\frac {\partial w_{i}}{\partial w_{j}}}{\dot {w}}_{j}}$, j ∈ {i の先行ノード}

例として次の関数を考える。

${\displaystyle {\begin{aligned}y&=f(x_{1},x_{2})\\&=x_{1}x_{2}+\sin x_{1}\\&=w_{1}w_{2}+\sin w_{1}\\&=w_{3}+w_{4}\\&=w_{5}\end{aligned}}}$

それぞれの部分式を中間変数 ${\displaystyle w_{i}}$ としてラベル付けした。最初に ${\displaystyle w_{1}=x_{1},w_{2}=x_{2}}$ としている。

どの入力変数で偏微分するかによって ${\displaystyle {\dot {w}}_{1}}$ や ${\displaystyle {\dot {w}}_{2}}$ の初期値が異なる。${\displaystyle x_{1}}$ に関する偏微分を計算する場合の初期値は、

${\displaystyle {\begin{aligned}{\dot {w}}_{1}={\frac {\partial w_{1}}{\partial x_{1}}}={\frac {\partial x_{1}}{\partial x_{1}}}=1\\{\dot {w}}_{2}={\frac {\partial w_{2}}{\partial x_{1}}}={\frac {\partial x_{2}}{\partial x_{1}}}=0\end{aligned}}}$

となる。初期値が決まったら下の表に示す連鎖律に従って各偏導関数値を順に計算していく。図2はこの処理を計算グラフとして表している。${\displaystyle {\dot {w}}_{5}={\tfrac {\partial y}{\partial x_{1}}}}$ が求めたい値である。

${\displaystyle {\begin{array}{l|l}{\text{Operations to compute value}}&{\text{Operations to compute derivative}}\\\hline w_{1}=x_{1}&{\dot {w}}_{1}=1{\text{ (seed)}}\\w_{2}=x_{2}&{\dot {w}}_{2}=0{\text{ (seed)}}\\w_{3}=w_{1}\cdot w_{2}&{\dot {w}}_{3}=w_{2}\cdot {\dot {w}}_{1}+w_{1}\cdot {\dot {w}}_{2}\\w_{4}=\sin w_{1}&{\dot {w}}_{4}=\cos w_{1}\cdot {\dot {w}}_{1}\\w_{5}=w_{3}+w_{4}&{\dot {w}}_{5}=1\cdot {\dot {w}}_{3}+1\cdot {\dot {w}}_{4}\end{array}}}$

この関数 f に対する勾配を求めるためには ${\displaystyle {\tfrac {\partial y}{\partial x_{1}}}}$ だけではなく ${\displaystyle {\tfrac {\partial y}{\partial x_{2}}}}$ も求める必要がある。そのため、初期値を ${\displaystyle {\dot {w}}_{1}=0;{\dot {w}}_{2}=1}$ とした同様の計算を追加で行わなければならない。

勾配を求める場合に必要なボトムアップ型自動微分の実行回数は入力変数の個数と等しく、トップダウン型自動微分では出力変数の個数に等しい。ボトムアップ型やトップダウン型の自動微分を1回行うのに必要な計算量は、元のプログラムの計算量に比例する。そのため、偏微分する関数f : ℝⁿ → ℝ^m が n ≪ m を満たす場合、ボトムアップ型自動微分はトップダウン型自動微分よりも効率的である。

トップダウン型自動微分

トップダウン型自動微分では、はじめに偏微分される出力変数を固定して、それぞれの部分式に関する偏導関数値を再帰的に計算する。手計算においては部分式を連鎖律における外側の関数の偏微分で繰り返し置き換えていくことに相当する。

${\displaystyle {\frac {\partial y}{\partial x}}={\frac {\partial y}{\partial w_{1}}}{\frac {\partial w_{1}}{\partial x}}=\left({\frac {\partial y}{\partial w_{2}}}{\frac {\partial w_{2}}{\partial w_{1}}}\right){\frac {\partial w_{1}}{\partial x}}=\left(\left({\frac {\partial y}{\partial w_{3}}}{\frac {\partial w_{3}}{\partial w_{2}}}\right){\frac {\partial w_{2}}{\partial w_{1}}}\right){\frac {\partial w_{1}}{\partial x}}=\cdots }$

トップダウン型自動微分において、求める値はボトムアップ型の随伴^{[訳語疑問点]}であり、上線 ${\displaystyle {\bar {w}}_{i}}$ で表す。これは中間変数 ${\displaystyle w_{i}}$ に関する偏微分

${\displaystyle {\bar {w}}_{i}={\frac {\partial y}{\partial w_{i}}}}$

である。連鎖律より、${\displaystyle w_{i}}$ が計算グラフで後続ノードを持つ場合、以下のように計算できる。${\displaystyle {\bar {y}}}$ は1で、y以外のノードで後続ノードがなければ0になる。

${\displaystyle {\bar {w}}_{i}=\sum _{j}{\bar {w}}_{j}{\frac {\partial w_{j}}{\partial w_{i}}}}$, j ∈ {i の後続ノード}

トップダウン型自動微分は連鎖律を外側から内側（図3の計算グラフでは上から下）にたどっていく。

偏微分する関数f : ℝⁿ → ℝ^m が n ≫ mを満たすとき、トップダウン型自動微分はボトムアップ型自動微分よりも効率的である。例示した関数は m = 1 のスカラー値関数（1つだけ値を返す関数）なので、勾配を計算するには計算グラフを一度たどるだけでよい。これは n = 2回計算グラフをたどる必要があったボトムアップ型自動微分の計算量の半分である。

しかし、トップダウン型自動微分は、テープやWengert リスト^[6]（なお、Wengert はボトムアップ型を1964年に発表したが^[4]、トップダウン型を発表したわけではない）と呼ばれるサイズ変更が可能な配列に中間変数 ${\displaystyle w_{i}}$ の計算結果を追記していく必要があるためメモリ使用量の点で不利であり、計算グラフが巨大になるとメモリ使用量が問題となる可能性がある。この問題は保存する中間変数を限定し、必要な中間変数を再計算することによって軽減される。

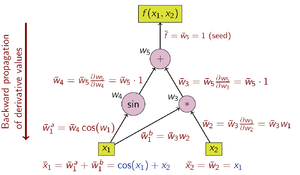
トップダウン型自動微分を用いて偏導関数値を計算するための演算は以下の通りである（関数値を求める時と順番が逆であることに注意）。${\displaystyle {\bar {w}}_{1}={\tfrac {\partial y}{\partial x_{1}}}}$ と ${\displaystyle {\bar {w}}_{2}={\tfrac {\partial y}{\partial x_{2}}}}$ が求めたい値である。

${\displaystyle {\begin{array}{l}{\text{Operations to compute derivative}}\\\hline {\bar {w}}_{5}=1{\text{ (seed)}}\\{\bar {w}}_{4}={\bar {w}}_{5}\cdot 1\\{\bar {w}}_{3}={\bar {w}}_{5}\cdot 1\\{\bar {w}}_{2}={\bar {w}}_{3}\cdot w_{1}\\{\bar {w}}_{1}={\bar {w}}_{3}\cdot w_{2}+{\bar {w}}_{4}\cdot \cos w_{1}\end{array}}}$

最後の ${\displaystyle {\bar {w_{1}}}}$ は以下の理由で成立する。図3で ${\displaystyle x_{1}=w_{1}}$ から ${\displaystyle w_{3}}$ と ${\displaystyle w_{4}}$ に矢印が引かれていることより、${\displaystyle w_{3}}$ と ${\displaystyle w_{4}}$ は ${\displaystyle w_{1}}$ の後続ノードである。合成関数の偏微分の連鎖律より ${\displaystyle {\bar {w_{1}}}={\bar {w_{3}}}{\frac {\partial w_{3}}{\partial w_{1}}}+{\bar {w_{4}}}{\frac {\partial w_{4}}{\partial w_{1}}}}$ であり、後は ${\displaystyle w_{3}}$ と ${\displaystyle w_{4}}$ の定義を代入すれば良い。どの中間変数がどの中間変数に影響を及ぼすか記録する必要がある。

テープを使用しない場合は、以下のように Python で実装できる。

import math

class Var:
    def __init__(self, value, children=None):
        self.value = value
        self.children = children or []
        self.grad = 0

    def __add__(self, other):
        return Var(self.value + other.value, [(1, self), (1, other)])

    def __mul__(self, other):
        return Var(self.value * other.value, [(other.value, self), (self.value, other)])

    def sin(self):
        return Var(math.sin(self.value), [(math.cos(self.value), self)])

    def calc_grad(self, grad=1):
        self.grad += grad
        for coef, child in self.children:
            child.calc_grad(grad * coef)

# 例: f(x, y) = x * y + sin(x)
x = Var(2)
y = Var(3)
f = x * y + x.sin()

# 偏微分の計算
f.calc_grad()

print("f =", f.value)
print("∂f/∂x =", x.grad)
print("∂f/∂y =", y.grad)

テープを使用する場合のアルゴリズムの実装の流れは以下の通りである。

1. テープをサイズ変更が可能な動的配列として用意する。テープの要素は中間変数 ${\displaystyle w_{i}}$ 毎に作り、以下の5項目を記録する。
   1. 計算内容（足し算や掛け算など）
   2. 計算グラフの入辺：計算に使用した引数のテープ上のインデックスのリスト。${\displaystyle w_{3}}$ なら ${\displaystyle w_{1}}$ と ${\displaystyle w_{2}}$。
   3. 計算グラフの出辺：この中間変数がどの計算で使われたかのテープ上のインデックスのリスト。計算しながら追記していく。${\displaystyle w_{1}}$ なら ${\displaystyle w_{3}}$ と ${\displaystyle w_{4}}$。
   4. ${\displaystyle w_{i}}$ の値
   5. ${\displaystyle {\bar {w}}_{i}}$ の値（最初は未定）
2. ${\displaystyle w_{i}}$ の値を計算していく。その際、上記の内容をテープに追記していく。また、テープには、どの中間変数の計算で、どの中間変数を使用したかも追記する（上記の3番）。同一の中間変数を2回以上計算しないように注意が必要。
3. テープの最後の ${\displaystyle {\bar {w}}_{i}}$ を 1 として、その1つ前から逆順に ${\displaystyle {\bar {w}}_{i}=\sum _{j}{\bar {w}}_{j}{\frac {\partial w_{j}}{\partial w_{i}}}}$ を計算していく。

スカラー値ではなく NumPy のような多次元配列（テンソル）を扱う場合も処理すべき内容は同じである。${\displaystyle {\bar {w}}_{j}{\tfrac {\partial w_{j}}{\partial w_{i}}}}$ を1つの処理単位として実装する。これを vector-Jacobian product (VJP) や L-operator (Lop) と言う^{[7][8][9][10]}。行列積の VJP は行列積で実装できる。ただし、ある軸での和（NumPyのsum）の VJP は、その軸で値を繰り返して ${\displaystyle {\bar {w}}_{j}}$ の軸を復元する処理になるなど、直観的で無い物もある。ハーバード大学の HIPS が開発していた Autograd^[11] は、ほぼ全ての NumPy の関数の VJP を実装していて、簡潔に実装しているので参考になる。なお ${\displaystyle {\tfrac {\partial w_{i}}{\partial w_{j}}}{\dot {w}}_{j}}$ は Jacobian-vector product (JVP) や R-operator (Rop) と言い、ボトムアップ型で使用する。

例えば、行列積の vector-Jacobian product (VJP) の場合は、以下のように求める。${\displaystyle Z=XY}$ を考え、${\displaystyle {\bar {X}}}$ を求める。行列積を行列の要素で表記する。

${\displaystyle z_{ik}=\sum _{j}x_{ij}y_{jk}}$

どの要素がどの要素に影響を及ぼしているか注意を払い、${\displaystyle {\bar {x}}_{pq}}$ を求める。

${\displaystyle {\bar {x}}_{pq}=\sum _{r}{\bar {z}}_{pr}{\frac {\partial z_{pr}}{\partial x_{pq}}}=\sum _{r}{\bar {z}}_{pr}{\frac {\partial x_{pq}y_{qr}}{\partial x_{pq}}}=\sum _{r}{\bar {z}}_{pr}y_{qr}}$

これを要素表記から行列表記に直すと、転置行列との行列積になる。

${\displaystyle {\bar {X}}={\bar {Z}}Y^{T}}$

二重数を用いた自動微分

ボトムアップ型自動微分は実数の代数に（元を）添加して新しい算術を導入することによって可能である。全ての数（通常の実数）に対して、その数における関数の微分を表現する追加の成分が足され、全ての算術演算がこの添加代数に拡張される。すなわち二重数の代数である。このアプローチはプログラミング空間上の演算子法（英語版）の理論（つまり双対空間のテンソル代数）によって一般化される（解析的プログラミング空間（英語版）を見よ)。

各数 ${\displaystyle x}$ を数 ${\displaystyle x+x'\varepsilon }$ に置き換える。ここで ${\displaystyle x'}$ は実数だが、${\displaystyle \varepsilon }$ は ${\displaystyle \varepsilon ^{2}=0}$ を満たす抽象的数（英語版）である（無限小；滑らかな無限小解析も参照）。ちょうどこれだけを用いて通常の演算が得られる：

${\displaystyle {\begin{aligned}(x+x'\varepsilon )+(y+y'\varepsilon )&=x+y+(x'+y')\varepsilon \\(x+x'\varepsilon )\cdot (y+y'\varepsilon )&=xy+xy'\varepsilon +yx'\varepsilon +x'y'\varepsilon ^{2}=xy+(xy'+yx')\varepsilon \end{aligned}}}$

引き算と割り算についても同様である。

いまやこの拡張算術のもとで多項式を計算できる。もし ${\displaystyle P(x)=p_{0}+p_{1}x+p_{2}x^{2}+\cdots +p_{n}x^{n}}$ ならば、

${\displaystyle {\begin{aligned}P(x+x'\varepsilon )&=p_{0}+p_{1}(x+x'\varepsilon )+\cdots +p_{n}(x+x'\varepsilon )^{n}\\&=p_{0}+p_{1}x+\cdots +p_{n}x^{n}+p_{1}x'\varepsilon +2p_{2}xx'\varepsilon +\cdots +np_{n}x^{n-1}x'\varepsilon \\&=P(x)+P^{(1)}(x)x'\varepsilon \end{aligned}}}$

ここで ${\displaystyle P^{(1)}}$ は ${\displaystyle P}$ の最初の引数に対する微分であり、${\displaystyle x'}$（種と呼ばれる）は任意に取れる。

上に述べたように、この新しい算術は、順序対（${\displaystyle \langle x,x'\rangle }$ と書かれる元）と、最初の成分に対しては通常の算術を、第二の成分に対しては一階微分の算術を、それぞれ与えたものからなる。多項式に関する上の結果を解析関数に広げれば、新しい算術に対する、基本的な算術と幾つかの標準的な関数のリストが得られる：

${\displaystyle {\begin{aligned}\left\langle u,u'\right\rangle +\left\langle v,v'\right\rangle &=\left\langle u+v,u'+v'\right\rangle \\\left\langle u,u'\right\rangle -\left\langle v,v'\right\rangle &=\left\langle u-v,u'-v'\right\rangle \\\left\langle u,u'\right\rangle *\left\langle v,v'\right\rangle &=\left\langle uv,u'v+uv'\right\rangle \\\left\langle u,u'\right\rangle /\left\langle v,v'\right\rangle &=\left\langle {\frac {u}{v}},{\frac {u'v-uv'}{v^{2}}}\right\rangle \quad (v\neq 0)\\\sin \left\langle u,u'\right\rangle &=\left\langle \sin(u),u'\cos(u)\right\rangle \\\cos \left\langle u,u'\right\rangle &=\left\langle \cos(u),-u'\sin(u)\right\rangle \\\exp \left\langle u,u'\right\rangle &=\left\langle \exp u,u'\exp u\right\rangle \\\log \left\langle u,u'\right\rangle &=\left\langle \log(u),u'/u\right\rangle \quad (u>0)\\\left\langle u,u'\right\rangle ^{k}&=\left\langle u^{k},ku^{k-1}u'\right\rangle \quad (u\neq 0)\\\left|\left\langle u,u'\right\rangle \right|&=\left\langle \left|u\right|,u'{\mbox{sign}}u\right\rangle \quad (u\neq 0)\end{aligned}}}$

一般に、プリミティヴの関数 ${\displaystyle g}$ に対して、

${\displaystyle g(\langle u,u'\rangle ,\langle v,v'\rangle )=\langle g(u,v),g_{u}(u,v)u'+g_{v}(u,v)v'\rangle }$

ここで ${\displaystyle g_{u}}$ と ${\displaystyle g_{v}}$ はそれぞれ ${\displaystyle g}$ の最初と2番目の引数に対する微分である。

基本的な二項算術演算を（実数と二重数の）混在した引数に対して、つまり順序対 ${\displaystyle \langle u,u'\rangle }$ と実数 ${\displaystyle c}$ に対して適用するとき、まずこの実数を ${\displaystyle \langle c,0\rangle }$ に引き上げる（lifting）。関数 ${\displaystyle f:\mathbb {R} \rightarrow \mathbb {R} }$ の ${\displaystyle x_{0}}$ に於ける微分はいまや ${\displaystyle f(\langle x_{0},1\rangle )}$ に上の算術を使って計算することによって得られる。これは ${\displaystyle \langle f(x_{0}),f'(x_{0})\rangle }$ を結果として与える。

ベクトル引数と関数

多変数関数は、方向微分作用素を用いることで、一変数関数の場合と同様の効率と仕組みで取り扱える。つまり、${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}}$ の ${\displaystyle x\in \mathbb {R} ^{n}}$ における ${\displaystyle x'\in \mathbb {R} ^{n}}$ 方向微分 ${\displaystyle y'=\nabla f(x)\cdot x'}$ を計算したい場合、それは ${\displaystyle (\langle y_{1},y'_{1}\rangle ,\ldots ,\langle y_{m},y'_{m}\rangle )=f(\langle x_{1},x'_{1}\rangle ,\ldots ,\langle x_{n},x'_{n}\rangle )}$ を上と同様の算術を使って計算すればよい。もし ${\displaystyle \nabla f}$ の全ての要素が望みならば、${\displaystyle n}$ 個の関数評価が要求される。ここで、多くの最適化アプリケーションでは、実際には方向微分があれば十分である。

高階・多変数

上の算術は多変数関数の二階やもっと高階の微分の計算の為に一般化出来る。しかし、その算術規則は直ちに極めて複雑なものとなる：複雑性は最高次の微分の次数に対して二次関数的となる。その代わりに、途中で打ち切った（truncated）テイラー多項式の代数を使用できる。結果得られる算術（一般化された二重数の上で定義された）は、関数を新しいデータ型であるかのように使って、効率的に計算することを可能にする。ひとたび関数のテイラー多項式が分かれば、その導関数たちは容易に抽出できる。 厳密で一般的な定式化はテンソル級数展開（英語版）を通してプログラミング空間上の演算子法（英語版）を用いることにより達成される。

実装

自動微分の実装方法には大きく分けて、ソースコードの変換とオペレータオーバーローディングによる方法の2つがある。

ソースコード変換

関数値を求める関数を記述した元のソースコードから、偏導関数値を計算する処理を含んだプログラムを自動的に生成する手法である。ソースコード変換はあらゆるプログラミング言語で実装でき、コンパイル時の最適化を行いやすいが、自動微分ツールの作成は難しい。

オペレータオーバーローディング

この手法は演算子のオーバーロードがサポートされているプログラミング言語で記述されたソースコードに対してのみ適用可能である。元のソースコードの流れを大きく変更することなく実現できるが、基本データ型の変更などの小さな変更は必要である。

ボトムアップ型自動微分をオペレータオーバーロードで実現するのは容易である。トップダウン型自動微分についても可能であるが、現状のコンパイラではボトムアップ型自動微分と比べると最適化の面で不利である。

ソフトウェア

自動微分を実装したライブラリなどのソフトウェアが多数存在する。2010年代の第3次人工知能ブームの際にディープラーニングに自動微分が必要なため、TensorFlowやPyTorchなどトップダウン型の自動微分を含むライブラリが多数作られた。

脚注

参考文献

• 久保田, 光一; 伊理, 正夫 (1998). アルゴリズムの自動微分と応用. 現代非線形科学シリーズ. 3. コロナ社. ISBN 978-4339026023 
• 伊理正夫、「高速自動微分法(第2回年会特別講演)」『応用数理』 1993年 3巻 1号 p.58-66, doi:10.11540/bjsiam.3.1_58, 日本応用数理学会
• Rall, Louis B. (1981). Automatic Differentiation: Techniques and Applications. Lecture Notes in Computer Science. 120. Springer. ISBN 3-540-10861-0 
• Griewank, Andreas; Walther, Andrea (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Other Titles in Applied Mathematics. 105 (2nd ed.). SIAM. ISBN 978-0-89871-659-7. http://www.ec-securehost.com/SIAM/OT105.html 
• Neidinger, Richard (2010). “Introduction to Automatic Differentiation and MATLAB Object-Oriented Programming”. SIAM Review 52 (3): 545–563. doi:10.1137/080743627. http://academics.davidson.edu/math/neidinger/SIAMRev74362.pdf 2013年3月15日閲覧。. 

外部リンク

• www.autodiff.org - Community Portal for Automatic Differentiation